Binary and Hexidecimal Number Systems
Computers are very stupid electronic boxes and more than one computer specialist has noted that much of our world now depends on circuitry that can’t count to two. However, they do understand electrical signals that can be either “on” or “off”. The binary system represents electrical signals with “0” representing no electrical pulse on a wire and “1” representing a pulse of electricity on the wire.
Binary Number System
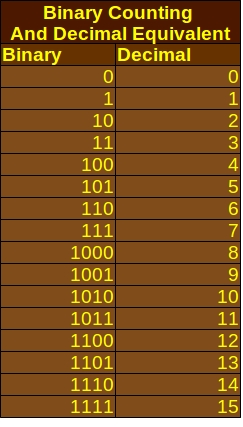
Binary values can be arranged to represent any number in the decimal system that makes sense to everybody. Computer and networking specialists make use of the following table to convert binary values to decimal.
The above table represents how far a computer specialist usually has the table memorized, but it can stretch off to the left as far as necessary. As you can see, each value is the double of the one to the right because binary-to-decimal calculations are heavily involved in powers of two (2X). For each binary value that is added to the left side, the number of its “place value” is doubled. Now we can add some ones and zeros to that chart:
To convert this binary number, 11010000, into decimal, simply take the columns that have ones in the binary cell and add the decimal numbers. 128 + 64 + 16 = 208. So the binary number 11010000 converts to 208. Converting a decimal number into binary is the process in reverse. You start with the largest power of two that can be subtracted from the number and get a non-zero, positive number. For instance, to convert 255 into a binary number, start at the largest power of 2 that goes into it. (Hint: It’s not 29). That number should be 128, so put a one in that slot and subtract 128 from your number to get 127. Repeat the process until you reach zero. The result should be 11111111.
It is possible to count in binary, with each binary number corresponding with a decimal number:
[mtouchquiz 3]
Hexidecimal Number System
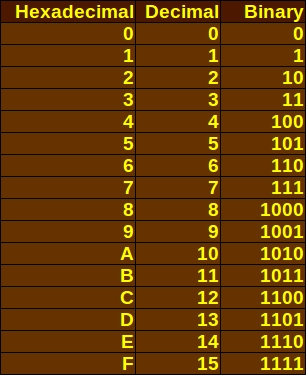
Hexidecimal (Hex) is another numbering system that uses 16 digits, the familiar 0-9 plus the letters A-F. Each hexidecimal digit has a corresponding decimal number and four-digit binary number, as shown in the chart below:
Hexidecimal is a more human-readable counting system that works in multiples of 16, such as 1 X 16 = 16, 16 X 16 = 256, 256 X 16 = 4096 and so on. Counting in Hex might be a little baffling at first because most people are used to thinking in multiples of 10, not 16. The digits in Hex go like:
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 20 21 22…
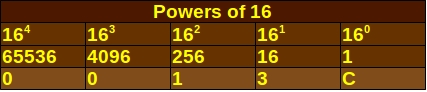
And so on, for as long as you need to count. It’s not likely to earn you a good grade in math class unless you are studying computer mathematics, but it’s workable for networking purposes. Each digit has a corresponding power of 16 as shown in the chart below:
Hex can be converted into binary and decimal and vice versa as necessary. To convert binary into Hex, it is easier to break up longer binary strings into groups of four bits. 11000110 becomes 1100 0110, which converts to decimal as 12 6. The decimal number 12 corresponds to C in Hexidecimal and the number 6 in decimal corresponds with 6 in Hexidecimal. So 11000110 in binary is the equivalent of C6 in hexidecimal.
To convert from Hexidecimal to binary, simply follow the same process in reverse. It may be easier to have a powers-of-16 chart handy if you get into the larger hexidecimal numbers or are just beginning with Hexidecimal. A Hex number such as 13C can be broken down with a chart like this one, with one digit in each column:
Which translates in plain English as: 1 times 256, plus 3 times 16, plus 12 times 1. Follow the order of operations familiar from math class and do the multiplication first: 256 + 48 + 12. This should give you the decimal number 316. Then, it is a simple matter to use a decimal-to-binary conversion chart to break down the number into its binary form: 100111110.
[mtouchquiz 4]
How Important Are Binary and Hexadecimal?
Binary and Hexadecimal are important enough that you won’t be able to get your CCNA certification without knowing how to convert from one to the other and from both to decimal. So it helps to at least be able to make out an accurate conversion chart that can handle all three numbering systems. Remember that computers can only understand bits, so you might see a subnet mask of 255.255.255.0, but the computer sees it as, 11111111.11111111.11111111.00000000.
Everything You Ever Wanted To Know About Number Systems in One Book
More Supplies for the Network Specialist
[simple-rss feed=”http://rest.ebay.com/epn/v1/find/item.rss?keyword=CCNA+Certification+-hacker&categoryId1=58058&sortOrder=BestMatch&programid=1&campaignid=5337337555&toolid=10039&listingType1=All&lgeo=1&feedType=rss” limit=5]