Scientific Notation
What Is Scientific Notation?
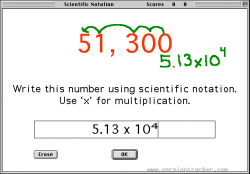 Yourdictionary.com defines Scientific Notation as a mathematical expression used to represent any decimal number as a number between one and ten raised to a specific power of ten. This allows scientists and other people who work with very big and very small numbers to handle them without having to write down a lot of digits. Examples of scientific numbers: 4X10^6, 3.6X10^5, and 8.51X10^-6. These represent 4,000,000, 360,000, and 0.00000851, respectively. (The ^ symbol represents what power 10 is raised to. You can find it on any scientific or graphing calculator and sometimes even on that calculator on your computer.)
Yourdictionary.com defines Scientific Notation as a mathematical expression used to represent any decimal number as a number between one and ten raised to a specific power of ten. This allows scientists and other people who work with very big and very small numbers to handle them without having to write down a lot of digits. Examples of scientific numbers: 4X10^6, 3.6X10^5, and 8.51X10^-6. These represent 4,000,000, 360,000, and 0.00000851, respectively. (The ^ symbol represents what power 10 is raised to. You can find it on any scientific or graphing calculator and sometimes even on that calculator on your computer.)
The Khan Academy on Scientific Notation
 So, who uses scientific notation?
So, who uses scientific notation?
- Mathematicians use scientific notation a lot. They have to. It saves time over having to write big or small numbers.
- Astronomers use it when measuring distances to other stars and galaxies. Even when you measure things in parsecs, numbers can get pretty huge.
- Physicists use it to measure the distance between particles. These measurements are usually very small numbers.
- Geologists use it to measure the age of rocks.
How To Use Scientific Notation
It’s easy: You just move the decimal point. Let’s take a simple number: 1,000,000. That’s a one and six zeros. You want to get a number between one and ten, so you pick up the implied decimal point after the last zero and move it to the left until it’s next to the one. (1.000000) How many zeros did you jump over? That’s the exponent of 10 you use.
The number should now look like this: 1X10^6. That’s 1 times 10 to the power of 6 or, as another way of putting it, 1 X 10 X 10 X 10 X 10 X10 X 10.
Now the other way: Very small numbers. Let’s take 0.0125. Again, you want to move the decimal point so you have a number between one and 10. That means moving it the other way, to the right, so that you have 1.25. The decimal point moved two places…But this is where scientific notation can get a little tricky. Because you moved it to the right, the exponent of 10 has to be a negative number. The correct answer is 1.25X10^-2.
What is an exponent, anyway? The number after the ^ symbol tells you how many times to multiply a number by itself. 10^1 is simply 10; 10^2 is ten times ten, or 100. 10^3 is 10 times 10 times 10, or 1000.
Give It A Quick Try
1,250 in Scientific Notation
.00157 in Scientific Notation
Now the other way…
What do you do when you see a number in scientific notation? Simple; you just reverse the process. Let’s say you have 1.25 X 10^7. Remember, the power of 10 is how far to the left or right the decimal has moved. In this case, the decimal point has been moved to the left 7 times. So, to get it out of scientific notation, you just have to move it back to the right that many places. Moving it two places gives you 125, so you have to add some zeros. Since 7 minus 2 equals 5, that means you add 5 zeros to get 12,500,000.
And what if you have a negative exponent? Well, let’s say you have 1 X 10^-3. That means you take the decimal point and move it to the left three places. It becomes 0.001.
A Quick Try
1.37 X 10^4
1.05 X 10^-2
Adding and Subtracting in Scientific Notation
Adding and subtracting in Scientific Notation is very similar to adding and subtracting fractions. You have to adjust the exponent of 10 for both numbers so that they match before you do anything else. For example:
2.1 X 10^5 + 3.4 X 10^6
You can adjust either the first or the second number. If you adjust the first, you have to move the decimal point in 2.1 to the left one digit so it becomes 0.21 and also add one to the exponent so it becomes ^6. It now looks like this:
0.21X10^6 + 3.4 X 10^6
Now it becomes a simple matter of adding 0.21 and 3.4. This is 3.61. Since 3.61 is less than 10 and greater than 1, you can simply add the power of 10. Your answer looks like this:
3.61 X 10^6
If you subtract two numbers in scientific notation, it’s basically the same thing except you subtract. For example:
7 × 10^5 – 5.2 × 10^4
First you change the exponents: 70 X 10^4 – 5.2 X 10^4
Then you subtract: (70 – 5.2) X 10^4 = 64.8 X 10^4
Then you convert back to scientific notation for your answer: 6.48 X 10^5
A Quick Try
5.25 X 10^3 + 6.2 X 10^4
1.2 X 10^4 - 7.3 X 10^3
Multiplying and Dividing in Scientific Notation
The steps in multiplying in scientific notation:
- Multiply the numbers out front.
- Add the exponents.
- Adjust for proper scientific notation if necessary.
What this looks like:
(n x 10^a) X (m x 10^b) = (n · m) X 10^a+b, then adjust for scientific notation.
For example:
(5.5 X 10^3) X (3 X 10^2)
Take the numbers at the “front” of each scientific notation number and multiply them: 5.5 X 3 = 16.5
Then add the exponents: 3 + 2 = 5
This would give you 16.5 X 10^5, but now you have to adjust for “proper” scientific notation. The answer is 1.65 X 10^6.
To divide scientific notation, you just basically follow this formula:
(n X 10^x) / (m X 10^y) = (n / m) X 10^x-y
As an example:
(6.2 X 10^6) / (3.1 X 10 X 10^3)
First, you divide the numbers out front: 6.2 / 3.1 = 2
Then you subtract the exponents from 10^6 and 10^3: 6 – 3 = 3
So the answer is 2 X 10^3
A Quick Try
1.3 X 10^4 - 2.1 X 10^3
2.8 X 10^9 / 7.0 ^ 10^8
A Few Good Calculators